Метод на Шенън-Фано

Независимо и едновременно е предложен от Клод Шенън (Bell Labs) и Р.М. Фано (MIT).

Шенън-Фано

Методът изисква да са известни вероятностите за срещането на всеки един символ в съобщението. На базата на тези вероятности се конструира таблица със следните характеристики:

- всеки символ се представя чрез код

- различните кодове имат различен брой битове

- кодовете за символи с по-ниска вероятност имат повече битове от тези с по-висока вероятност

- кодовете могат еднозначно да бъдат декодирани в символи

Алгоритъмът за конструриарне на таблицата работи по следния начин:


1. За симовлите се създава таблица с вероятността за тяхното срещане.

2. Таблицата се сортира според честотата на срещане, като символите с най-голяма вероятност са в началото на списъка.

3. Таблицата се разделя на две части, като броят на всички срещания на символите в първата й част е максимално близък до броя на всички срещания на символите от втората част.

4. При генерирането на кода на символите от първата част се присвоява нула, а на тези от втората част – единица.

5. Алгоритъмът се прилага рекурсивно, докато във всяка група остане само един символ.

Пример

Нека имам следните символи и техните вероятности

Символ

Срещания
Вероятност
a
32
1/2
b
16
1/4
c
8
1/8
d
4
1/16
e
2
1/32
f
2
1/32

Използвайки алгоритъма получаваме следните кодове:

Символ

Срещания
Вероятност
 итерация 1 итерация 2 итерация 3 итерация 4 итерация 6
a
32
1/2
0
b
16
1/4
1
0
c
8
1/8
1
1
0
d
4
1/16
1
1
1
0
e
2
1/32
1
1
1
1
0
f
2
1/32
1
1
1
1
1

 

Символ
Вероятност

Код
a
1/2
0
b
1/4
10
c
1/8
110
d
1/16
1110
e
1/32
11110
f
1/32
11111

След получаването на таблицата с кодове, пристъпваме към конструриране на декодиращото дърво на Шенън-Фано. То се използва, за да можем еднозначно да извличаме символи от потока входящи битове. За получената таблица със символи и кодове, декодиращото дърво изглежда така:

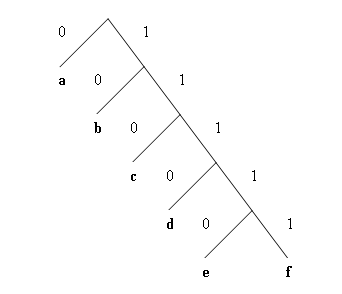
ВАЖНО

При алгоритъма на Шенън-Фано има един основен проблем. В случай на почти равно разделяне на групите по вероятности е възможно да възникнат две възможности, за конструиране на таблицата, което води до пораждане на различни дървета.

 

Пример

Нека имаме следната таблица с вероятности

Символ
Вероятност
a
0.20
b
0.20
c
0.20
d
0.15
e
0.15
f
0.10

Възможните таблици с кодове в случая са:

Таблица 1

Символ
Вероятност
 итерация 1 итерация 2 итерация 3
a
0.20
0
0
b
0.20
0
1
c
0.20
1
0
0
d
0.15
1
0
1
e
0.15
1
1
0
f
0.10
1
1
1

Таблица 2

Символ
Вероятност
 итерация 1 итерация 2 итерация 3
a
0.20
0
0
b
0.20
0
1
0
c
0.20
0
1
1
d
0.15
1
0
e
0.15
1
1
0
f
0.10
1
1
1

Таблица 3

Символ
Вероятност
 итерация 1 итерация 2 итерация 3
a
0.20
0
0
0
b
0.20
0
0
1
c
0.20
0
1
d
0.15
1
0
e
0.15
1
1
0
f
0.10
1
1
1

 

Цена на кода

Цена на кода се нарича величината, показваща средния брой битове необходими за кодирането на произволна буква от входното съобщение.

Цената на кода се изчислява като

L = n
∑
i = 1		 li.pi

Където:

li ( 1 ≤ i ≤ n ) е дължината на кода на буквата ai

pi е вероятността за срещане на ai

 

Оптимален код

Когато L приема минимална стойност, казваме че кодът строи оптимален подбуквен код за фиксирана азбука { a1, a2, ... an } с фиксирани честоти на срещане { p1, p2, ... pn }

Нека α е произволно входно съобщение с дължина d(α) (в брой букви). Тогава

d(α) n
∑
i = 1		 li.pi

ще бъде дължината (като очакван брой битове) на кодираното съобщение.

В нашия случай можем да изчислим очакваната дължина на съобщенията L1, L2, L3 съответно за Таблица 1, 2 и 3.

L1 = 2.0,2 + 2.0,2 + 3.0,2 + 3.0,15 + 3.0,15 + 3.0,10 = 2,60 бита

L2 = 2.0,2 + 3.0,2 + 3.0,2 + 2.0,15 + 3.0,15 + 3.0,10 = 2,65 бита

L3 = 3.0,2 + 3.0,2 + 2.0,2 + 2.0,15 + 3.0,15 + 3.0,15 = 2,65 бита

ВАЖНО

От L1< L2 и L3 следва един много важен извод: Алгоритъмът на Шенън-Фано не винаги строи оптимални кодове.

 
SAM - Science At Manchev.org
science.manchev.org